来源：瑞达期货

3数据与模型

本部分主要以香港恒生指数、恒指连续期货、恒指连续期权为代表，详细阐释对样本数据处理、计量统计检验、实证结论等，因台湾、韩国在样本数据处理、计量统计研究具有相似性，本文对该部分略省去，仅提供实证结果。本文采用的恒生指数、恒指连续期货、恒指连续期权、台湾加权指数、台指期货、台指期权及KOSPI200期货、KOSPI200期权等数据均来自DataStream。

   3.1数据处理

在计算股指期货、股指期权收益时，尤其是在处理期权数据时，往往涉及到单个合约成交持仓不活跃、合约具有不同到期日、不同种类（认沽权或认购权）、不同执行价格等原因，致使选择那个合约来计算收益存在困难。针对这个问题，不同学者采取不同处理方式，如，Manaster and Rendleman(1982)、Stephan and Whaley(1990)、魏洁（2013）等采取先计算出期权价格中隐含的现货指数，进而通过其隐含现货指数来计算收益。陈蓉（2011）则采用类似连续合约期权数据，但剔除收益率波动较大数据。针对本文研究需要，我们选取股指期货连续合约、股指期权（认购权）连续合约等数据，将其收益率定义为价格的自然对数的一阶差分，并剔除期指、期权在交割换月前后产生异常值。其收益率公式：

先以香港市场为研究对象，本文选取了2007年7月2日到2013年7月31日的香港恒生指数、恒生指数连续期货以及恒生指数连续期权数据，在剔除因合约移仓换月所产生的异常值，共获取1429个样本观察值。

3.2 恒生指数、恒生期指和恒指期权的统计特征

在探讨恒指、恒指期货和恒指期权品种间市场风险传递效应之前，本文首先对样本进行统计特性分析，其收益率序列统计结果见表1.2。其中 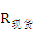代表恒生指数收益率序列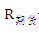， 代表恒指期货收益率序列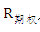， 为恒指期权收益率序列。   

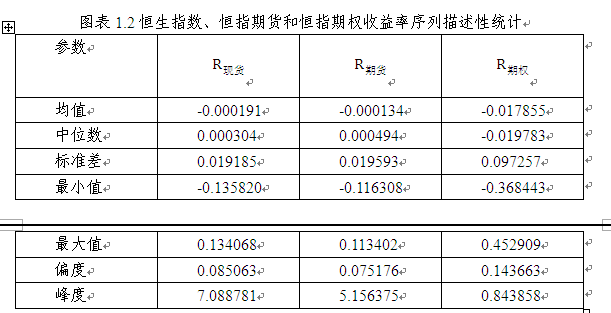
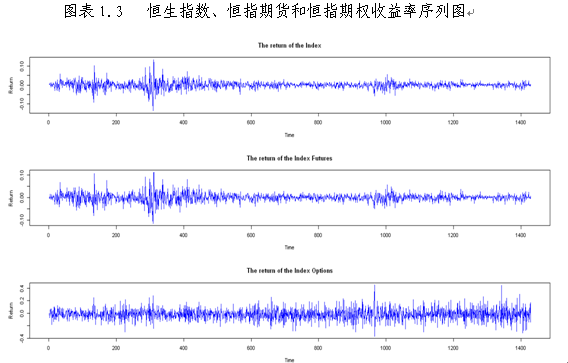
如上表1.2，恒指、恒指期货、恒指期权的收益率均为负值，这主要受到2008年次贷危机、欧洲债务危机等拖累，与近几年市场弱势有关。从标准差反映的风险程度来看，恒生指数、恒指期权、恒指期权收益率序列波动程度逐次增大，这表明衍生品杠杆在增加收益同时增加风险。从峰度、偏度来说，偏度均大于0，为右偏；峰度上，恒指与恒指期货是尖峰的，而恒指期权较为平缓。可见，恒指、恒指期货和恒指期权收益率序列为非正态分布。结合图表1.2和1.3收益率序列图，恒指、恒指期货、恒指期权具有长期均衡。而且恒指与恒指期货相关性，大于恒指与恒指期权和恒指期货与恒指期权。但恒指、恒指期货收益率序列呈现波动丛集性或波动的集中(volatility clustering or volatility pooling)特征，具有ARCH效应。 

3.3  计量统计检验

在建立模型之前需要对数据进行单位根检验、序列相关性检验及ARCH效应检验，以消除模型存在伪回归、序列相关性和ARCH效应等问题。在统计检验部分采用Eviews6.0统计软件。

3.3.1收益率序列平稳性检验

恒指、恒指期货和恒指期权因受各种因素影响，或呈现非平稳性特征。利用非平稳性数据时间序列建立模型将导致伪回归的问题，因而，需要首先对数据平稳性检验，本文采取ADF检验。

 单位根检验表明收益率序列在1%显著水平下拒绝存在单位根的假设，说明收益率序列是平稳的。这就保证所建立的模型不会存在伪回归的问题。

3.3.2收益率序列相关性检验

在考察是否存在序列自相关，采用Ljung-Box检验来检验各序列是否存在相关性，结果如下表1.5。

如上表，在5%的置信水平下，各序列均存在显著的自相关现象。

为消除序列相关，本文采用ARMA(p,q)模型， p，q分别取0至5，综合考虑AIC准则以及模型诊断，得到如下最优模型：

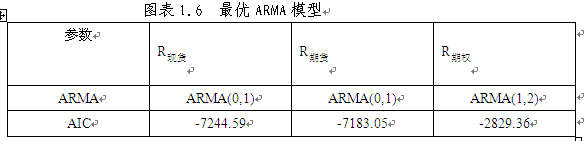
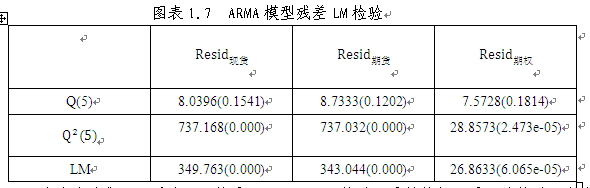
3.3.3  ARMA模型残差自相关性检验

对ARMA模型的残差序列进行自相关分析，发现模型能较好地消除序列的自相关，同时，为考虑滤波后的序列的波动特征，我们首先检验是否存在ARCH效应，结果如下：

3.4  DCC-MGARCH模型

Engle（2002）提出DCC-MGARCH模型（Dynamic Conditional Correlation Multivariate GARCH）是建立在CCC-GARCH模型(Constant Conditional Correlation GARCH)基础上, He，Luc et(2002,2006)对DCC-MGARCH模型进行再次扩展，形成（E）DCC-MGARCH模型（the Extended Dynamic Conditional Correlation Multivariate GARCH）。

      首先考虑一个由N个时间序列组成的系统，如，

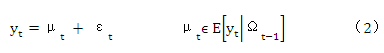
  其中 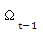是t-1时刻及之前所有相关信息的组合， ，

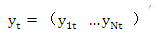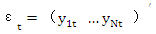 随机误差项的条件协方差矩阵可表示为： 

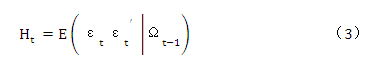
5结论与政策建议

  本文选取与中国内地资本市场发展相关的香港、台湾、韩国三地指数、指数期货和指数期权数据，采用扩展性DCC-MGARCH模型分析了各市场内的指数、指数期货和指数期权的跨品种之间风险传递效应。

   5.1 本文实证结论

  通过角度的扩展和模型方法上改进，我们得到以下主要结论：

（1）香港、台湾、韩国市场，其指数、指数期货和指数期权收益率序列呈在尖峰厚尾、有偏特征，且在残差具有明显的异方差特征， ARCH效应明显。目前，多元GARCH模型能更好刻画资本市场波动情况。

（2）结果显示，在三大市场内品种之间风险传递效应具有不尽一致的实证结果。

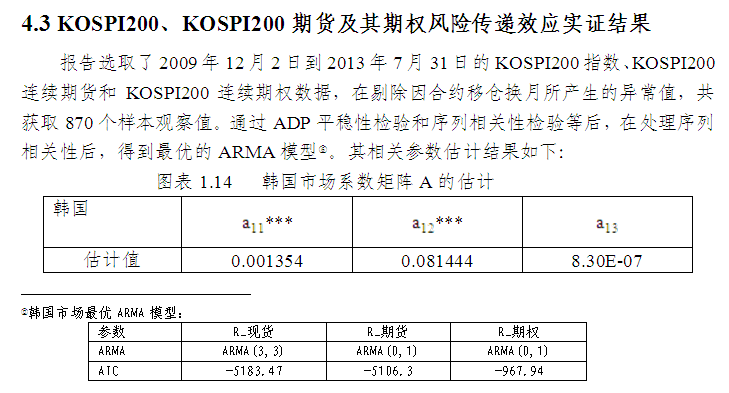
（a）股指期权风险传递效应方面，股指期权对股指期货和股指本身均不具有风险传递效应（魏洁等2013年则认为，香港恒指期货与恒指期权具有彼此不同的溢出效应；熊熊等认为KOSPI期权推出加大KOSPI期权、KOSPI指数的波动）。这表明，因股指期权在合约设计、投资者结构等差异，在特定的市场，使得具有相对独立性，不具有向其他品种或市场风险传递特性。但韩国与香港、台湾期权风险来源存在不同。结果显示，香港、台湾股指期权风险主要来自上期扰动信息风险遗留；而韩国KOSPI指数显著向其股指期权传递风险，来自指数风险传递效应（0.0057）明显小于小于上期系统性风险（0.80199）。

（b）股指期货风险传递效应方面，股指期货与股指期权虽同属于同一指数的衍生品，但二者不具有风险联动性，彼此相互独立。而且，股指期货均未增大其本身标的波动性，表明股指期货对外风险传递方面具有相对中立性。但三大市场股指期货市场波动都受到来自自身标的--股指的影响。结果表明，虽具备杠杆性、T+0等特征，但并未增加其他相关品种波动性。

（c）指数风险传递效应方面，股指均向股指期权当方面传递风险。来自韩国市场数据表明，股指向股指期权传递风险的效应，但向股指期权传递风险效应（0.0057）低于向股指期货传递效应（0.0129）。

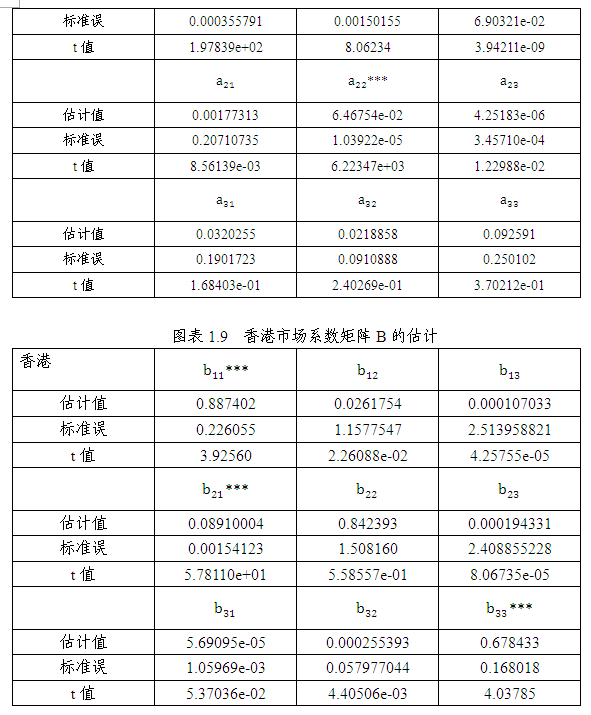
（3）在波动持续方面，香港、台湾、韩国三个市场单一品种系数加总均小于1，表明市场波动均具有暂时性，而非长期系统性。其中，波动性持久性最长的为香港恒生指数（0.070389486+0.01210599+0.887402=0.969897476）。

   5.2 政策建议

（1）因其高杠杆性、权利义务不对等等特性，如何控制其风险是监管者在推出股指期权最为关注问题，也是市场最为敏感的话题之一。其问题重心在于，股指期权是否增大向其他现有品种风险传递效应。但来自香港、台湾和韩国股指期权数据表明，股指期权和股指期货均不具有显著地向其他品种传递风险效应，这有助于减轻监管者对推出股指期权的担忧。另一方也表明，股指期货和股指期权具有对冲市场风险和管理市场波动率风险功能，能起到“稳定器”作用。因此，建议监管者在条件合适情况下宜加速推进沪深300股指期权上市的进程。

（2）基础市场的建设仍是关键。虽然数据区间并未发现恒指对恒指期权，台湾加权指数对台指期权的风险传递，但我们发现，股指均对股指期货，来自韩国市场的KOSPI指数对其指数期权的单向风险传递效应。这表明，降低股指期权（或股指期货）对市场所造成波动风险，首先需要加强衍生品标的指数-股市市场的建设，包括，提高上市公司质量，增强信息披露等等，股市市场建设才是根本。这也恰印证一句古谚，功夫在诗外。 

参考文献

[1] 陈蓉,曾海为.  波动率风险溢酬：基于香港和美国期权市场的研究[J]. 商业经济与管理,2012，（2）：54-59. 

[2] 董秀良,吴仁水. 基于DCC—MGARCH模型的中国A、B股市场相关性及其解释[J]. 中国软科学,2008(7)

[3] 国务院.  金融业发展和改革“十二五”规划，2012.4 韩立岩, 魏洁.  股指期权对股指期货的促进作用:来自韩国的证据国际金融研究2009,(3)

[4] 胡东滨,张展英. 基于 DCC-GARCH 模型的金融期货市场与外汇、货币市场的动态相关性研究[J]. 数理统计与管理,2012,31(5)

[5] 姜昱,邢曙光. 基于DCC—GARCH—CVaR的外汇储备汇率风险动态分析[J]. 财经理论与实践, 2010,(2):16

[6]  王斌,徐晟.  股指期货对我国股票市场波动性影响的实证分析[J]. 中国证券期货，2010,(8)

[7] 王雪标,周维利,范庆珍.  我国原油价格与外国原油价格的波动溢出效应—基于DCC-MGARCH模型分析[J].  数理统计与管理 2012,(4):275-577 

[8]  魏洁,韩立岩.  股指期货与股指期权市场之间的风险_省略_来自香港恒生指数衍生品市场的证据[J]

[9]  邢精平.  股指期货：方案设计与运作分析[M]. 北京：中国财经出版社，2007

[10]  熊熊,张宇,张维,张永杰.  股指期权推出对股票市场和股指期货市场波动性影响：以[]  KOSPI200股指期权为例[J]. 系统工程理论与实践,2011, 31(5)

[11]  杨胜刚，汪探德. 全球股指期货与期权市场的发展动向及启示[J]. 国际金融研究，2006 :(11)

[12]  张蕾.  金融资产动态相关性方法及应用研究[D]. 厦门大学博士论文，2004

[13]  张宇.  股指期权推出对现货市场和股指期货市场影响研究[D]. 天津大学 2009

[14]  仲伟周，李丹等.  流动性风险管理及其决策支持研究，上证联合研究计划第十九期课题研究报告，2009

[15]  邹功达.  全球金融衍生产品市场的发展及其启示[J]. 国际金融研究. 2002(10)

[16]  布鲁克斯（Brooks,C.），邹宏元. 金融计量经济学导论[M]. 西南财经大学出版社

[17]  Bollerslev T. Modeling the coherence in short-run nominal exchange rates:a multivariate generalized ARCH model [J]. Review of Economics and Statistics, 1990, 72: 498-505.

[18]  Bollerslev T, Wooldridge JM. Quasi-maximum likelihood estimation and inference in dynamic models with time-varying covariances [J]. Econometric Reviews, 1992,11:143-172.

[19]  Bollerslev T., Engle RF, Wooldridge JM. A capital asset pricing model with time varying covariances [J]. Journal of Political Economy, 1988

[20]  Changli  He  a1, Timo  Ter？svirta.  MOMENT STRUCTURE OF A FAMILY OF FIRST-ORDER EXPONENTIAL GARCH MODELS,working paper,2002

[21]  Engle RF. Dynamic conditional correlation-a simple class of multivariate GARCH models[J]. []  Journal of Business and Economic Statistics, 2002, 20: 339-350.

[22]  GG Booth, G.Geoffrey. Price discovery in the German equity index derivatives markets [J]. Journal of Futures Markets，1999，（19）

[23]  Glosten LR, Jagannathan R, Runkle DE. On the relation between expected value and the volatility of the nominal excess return on stocks [J]. Journal of Finance, 1993, 48: 1779-1801.

[24]  Kang,J,Lee,C.An empirical investigation of the lead-lag relations of returns and volatilities among the KOSPI200spot,futures,and options markets and their explanations. Journal of Emerging Market Finance . 2006

[25]  Kroner FK, Ng VK. Modelling asymmetric comovements of asset returns [J]. The Review of Financial Studies, 1998, 11: 817-844.

[26] Luc bauwens et. Multivariate GARCH models: a survey[J].  Journal of Applied Econometrics,2006,26(1) 

[27] Premalata Shenbagaraman. Do futures and options trading increase stock market volatility,NSE Research Initiative paper, http: www.nse-india.com/content/research/Paper60.pdf,2003

[28] S Manaster, RJ Rendleman.  Option Prices as Predictors of Equilibrium Stock Prices[J].  The Journal of Finance ,1982,(37)

[29] Seung O N, Seung Y O, Hyun K K, Wu L. The time difference of a measurement unit in the lead-lag relationship analysis of Korean financial market [J]. International Review of Financial Analysis, 2008, 17(2):259-273.

[30] Suqin Gu, Gong, Xiaowei. Effect of Equity Index Futures Trading on Stock Market Volatility Evidence from China,working paper, http://papers.ssrn.com/sol3/papers.cfm?abstract_id=2255230，2012

[31] Tse YK, Tsui AKC. A multivariate GARCH model with time-varying correlations [J].Journal of Business and Economic Statistics, 2002, 20: 351-362.

[32] Zhong,Maosen,Darrat. Price Discovery and Volatility Spillovers in Index Futures Market: Some Evidence from  Mexico[J]. Journal of Bussiness & Economic Statistics.1995:vo1.13, pp.27-35.